
home
needs
local resources
comfort
safety & health
contact
reports
Fuel characterization
The first element in any consideration of the theory of stoves is the source of heat, and burning of wood is the source of interest in this work. The combustion process is intimately connected with the characteristics of the fuel. In this section we shall be exclusively concerned with these aspects.
The material assembled in this section is a very short summary of some of the more important characteristics of wood as they are applicable to our problem. For more details and additional references see Kanury and Blackshear (1970), Roberts (1971), and Shelton and Shapiro (1976).
Chemical Nature of Wood
Wood, a product of photosynthesis, is a complex chemical substance. Its major constituents are hemicellulose (a polysaccharide producing wood sugars), cellulose (a polymer glucosan), and lignin (a multiring organic compound). Lignin has a relatively low molecular weight (about 1000) compared to the other two constituents (which have a molecular weight of about 104. There is some variation in the relative abundance of these constituents in wood - but as a rough guideline we could take cellulose to account for 50% and the other two 25% each by weight.
The fuel technologist's interests are slightly different. He would like to
know the composition of heat source in terms of the elements that contribute
to its heating value and its air requirements for combustion. Such an
analysis is usually called the ultimate analysis. It can be expected that
this will be dependent to a certain extent on the type of wood. It is
customary to distinguish two broad classes of wood - the hardwoods and the
softwoods. In addition, if the fuel supply is planned alongside a
forest-based industry, say, timber or pulp production, tree barks are left
behind as waste, but have fuel value. Arola (1978) compiled averages of
ultimate analysis of numerous species of wood in the United States (The
author is not aware of a similar table for forest species that are special
to different parts of the world) from different sources; these data are
given in Table 1.
| H | C | N | O | S | Ash | |
| Hardwood | ||||||
| Wood | 6.4 | 50.8 | 0.4 | 41.8 | - | 0.9 |
| Bark | 6.0 | 51.2 | 0.4 | 37.9 | - | 5.2 |
| Softwood | ||||||
| Wood | 6.3 | 52.9 | 0.1 | 39.7 | - | 1.0 |
| Bark | 5.9 | 53.1 | 0.2 | 37.9 | - | 2.3 |
A striking feature of this table is the remarkable consistency among different types of wood as far as relative percentages of different constituent elements are concerned. For all practical purposes we can get away with the statement “wood is composed of carbon. oxygen, and hydrogen“. The pollution aspect of wood is more manageable in the sense that it has no sulfur and its ash content is rather small.
A third way of looking at the fuel composition is based on the so-called proximate analysis. Table 2 , again taken from Arola, illustrates such an analysis. Speaking in a lighter vein, wood is really a lot of gas! That is at least what one would conclude from the table. The proximate analysis is vital for the equipment designer since it determines the method by which air is to be supplied for efficient combustion.
Some Physical Properties of Wood
As far as our application goes there are three principal properties of wood that are of vital interest. These are moisture content, density, and calorific value. Two other properties that are of importance in understanding and formulating a theory for wood combustion are thermal conductivity and the mass diffusion coefficient. We will discuss these properties in this section.
Wood, being hygroscopic, can rarely be used for domestic applications in its
so-called oven-dry state; it will always have a certain amount of moisture.
Before presenting information on levels of moisture content, it is useful to
make a comment on the way information on moisture is presented. Most
technical literature reports moisture content on the basis of the oven-dry
weight of wood. Drying is accomplished in an oven maintained at a
temperature slightly higher than 100ºC. Earl (1975) recommends 104ºC.
The process is monitored by periodically
weighing the sample of wood. Oven–dry wood is said to have been obtained
when two successive weighings are equal to one another within a prescribed
limit.
| Volatile matter | Fixed carbon | Ash | |
| Hardwood | |||
| Wood | 77.3 | 19.4 | 3.2 |
| Bark | 76.7 | 18.6 | 4.6 |
| Softwood | |||
| Wood | 77.2 | 22.0 | 1.6 |
| Bark | 73.3 | 23.7 | 3.0 |
However quite often moisture contents are reported on the basis of wet wood.
We present both definitions below.
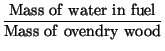 |
(1) | ||
 |
(2) |
It is easy to convert from one to another with the following formulas.
| (3) |
where ![]() and
and ![]() denote the fractions of moisture content on the
dry and wet basis. Whenever the moisture content is reported, it is
imperative to mention the basis of definition. When reports do not mention
it, the results of such work have to be treated with caution. An actual
question that is of interest is whether one should choose one definition in
preference to another. We shall provide an answer to this question slightly
later in this section.
denote the fractions of moisture content on the
dry and wet basis. Whenever the moisture content is reported, it is
imperative to mention the basis of definition. When reports do not mention
it, the results of such work have to be treated with caution. An actual
question that is of interest is whether one should choose one definition in
preference to another. We shall provide an answer to this question slightly
later in this section.
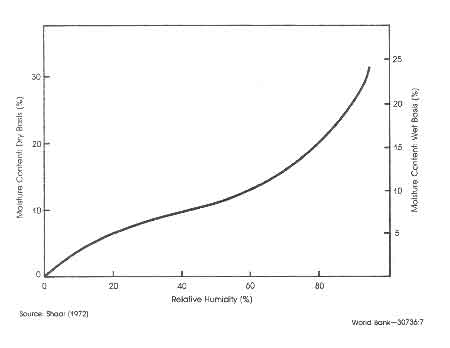
Figure:1 Effect of relative humidity on equilibrium moisture content of wood
A quantity that would be of particular interest is the moisture content in air-dried wood. In this connection wood technologists use the term equilibrium moisture content. It is defined as that moisture content of oven-dry wood after prolonged exposure to ambient conditions as a function of the humidity of the ambient and is shown in Fig.1 (Skar 1972). Earl (1975) states that air–dried wood will have an average moisture content of 25–30%. The drying process will take 2–3 months in the tropical regions. Faster drying and lower levels of moisture content could be obtained by adopting special solar driers (see for example, Hardie and Plumtre 1979).
We will now turn to the question of density. Wood is a porous substance. The porosityØ (ratio of the volume of pores to the volume occupied by the cell walls) of real woods lies in the range of 40–75%. Thus the specific gravity of wood can be expressed as
| (4) |
whereØ is a percentage. This formula is consistent with the measured values of specific gravity quoted by Shelton and Shapiro, i.e., in the range 0.31–0.88. Generally speaking, hardwoods are denser than softwoods. Needless to say the moisture content will have a significant influence on the density.
The specific combustion value is often considered the most important property of a fuel. But it is useful to remember that it is no more than a measure of the energy packed into a given quantity of fuel. While knowledge of it is vital to the design of combustion equipment, by no means is this sufficient for the successful design and operation of equipment.
The specific combustion value of some elementary fuels can be computed from thermodynamic data. For complex fuels such as wood, agricultural waste, etc., it can be approximately obtained from a knowledge of the ultimate analysis (see, for example, Wagner 1979). However, data on specific combustion values for most fuels are established by experimental methods. It is customary to distinguish between higher and lower specific combustion values, the difference between the two being that the former includes the latent heat of condensation of water vapor, an inevitable product of combustion of most fuels, including wood. Experimental determinations as well as data compilations are for the higher specific combustion value. But in most combustion equipment, the combustion products are exhausted into the atmosphere at a temperature that is higher than the condensation temperature of water vapor at atmospheric pressure. So it is the lower specific combustion value that is operative under such conditions.
Specific combustion values for the same classes of woods as those in Tables 1 and 2 are listed in Table 3 (Arola 1978). It is instructive to look at the numbers in the table with reference to the specific combustion values (in kilojoules/kilogram) of the most commonly used commercial.fuels: natural gas, 49,600; fuel oil, 41,800; coal, 27,800 to 30,200. As far as specific combustion values are concerned, wood does not fare badly in comparison to other fuels.
The existence of moisture affects the available heating values according to the following formula (Krishna Prasad 1983;
![$\displaystyle b_{m}=\left[ {\frac{1}{1+m_{d}}}\right] \left\{ b_{w}-(m_{d}+9x)\left[ (100-T_{o})C_{pw}+1\right] \right\}$](fuel/img14.png) |
(5) |
where the following notation is used; ![]() , specific combustion value of
moist wood (kJ/kg);
, specific combustion value of
moist wood (kJ/kg); ![]() , specific combustion value of oven dry wood
(kJ/kg);
, specific combustion value of oven dry wood
(kJ/kg); ![]() , mass fraction of hydrogen in wood; TØ
ambient temperature;
, mass fraction of hydrogen in wood; TØ
ambient temperature; ![]() , specific heat of water.(kJ/kgºC) and
, specific heat of water.(kJ/kgºC) and ![]() , specific latent heat of vaporization of water (kJ/kg).
, specific latent heat of vaporization of water (kJ/kg).
| Range | Average | |
| Hardwood | ||
| Wood | 17,600-20,700 | 19,900 |
| Bark | 16,100-23,900 | 18,700 |
| Softwood | ||
| Wood | 18,100-26,300 | 20,700 |
| Bark | 19,000-23,600 | 20,800 |
a In Kj/Kg; original data in BTU/lb have been converted to SI units and results rounded to third significant figure
Source: Arola (1978)
Fig.2 shows a schematic sketch of the way the heating value of wood can be
accounted for and Fig.3 shows a plot of Eq.5). In the graph ![]() = 19
MJ/kg and
= 19
MJ/kg and ![]() = 25ºC. The graph provides an explanation for
the difficulty experienced while lighting fires with moist wood.
Considerable energy has to be supplied to drive the moisture out. Only after
this process is completed will the wood ignite.
= 25ºC. The graph provides an explanation for
the difficulty experienced while lighting fires with moist wood.
Considerable energy has to be supplied to drive the moisture out. Only after
this process is completed will the wood ignite.
Another interesting feature emerges from a study of Table 3. On the average, the specific combustion values of hardwoods and softwoods do not differ by more than 10%. Yet one often hears the remark from fireplace owners that softwoods burn much faster than hardwoods. The explanation for this apparent contradiction lies in the fact that the specific gravity of different wood species can vary by a factor of 3. A fireplace of a given volumetric content will use up the light wood much faster than it does the heavy wood.
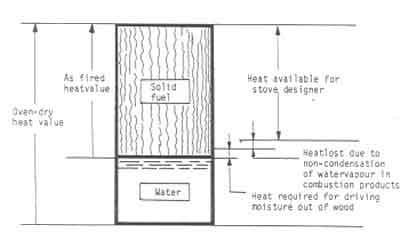
Figure:2 Schematic diagram illustrating the available heat from a piece of wood
The above argument has an important implication for designing a cookstove, as the following illustration shows. For the sake of argument, let us assume that we need a woodburning stove that is capable of supplying the same amount of heat to a cooking pot as a 1-kW electric surface heater does. Assuming that the electric stove works at an efficiency of 75% at the rated power output (see Goldemberg and Brown 1978) and the woodburning stove has an efficiency of 25%, the latter should have a power rating of 3kW, or should be capable of burning about 570g of oven-dry wood in an hour. The volume occupied by this wood be 633 cm³ at a specific gravity of 0.9 and 1900 cm³ at a specific gravity of 0.3. Therefore, satisfactory designs cannot be evolved without adequate information about the fuel to be used. Special care needs to be used when plans are being made to introduce stove designs that claim to use all kinds of fuels.
We return to the question posed earlier as to what basis we prefer for defining moisture content. We will use an example of fuelwood production and delivery chain (Leach and Gowen 1987). The situation is illustrated in Fig.4. Usually the forestry industry uses the volumetric unit (m³) for reporting the wood production.
A m³ of wood at the harvesting point in this example weighs
1265.8kg. The basic density of material is 600kg/m³ and the
oven-dry energy content is 20MJ/kg. md is 1.11 while ![]()
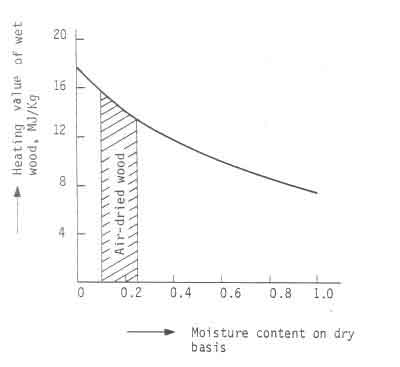
Figure:3 Heating value of wood as a function of moisture content
The air drying of wood can take place in two stages: between the point of harvesting and the point of purchase; and from the time of purchase to the time of use. Fig.4. records the changes in moisture content. It is obvious to note from the figure that the combustible material remains the same and so does the gross heating value. Thus it is advisable to report moisture content on the basis of oven-dry wood and this is the basis we use in further work in this book. As such in all further work we will suppress the subscript d while reporting moisture content.
We consider two other properties before we wind up this discussion. The first of these is thermal conductivity. Overall heat transfer in porous substances such as wood is expressed in terms of an "apparent“ conductivity to indicate that convection and radiation as well as true conduction contribute to the heat transfer process. Wood is also a strongly anisotropic substance and it is also established that the conductivity parallel to the grain is about twice that perpendicular to the grain. In general, conductivity of dry wood increases with density and moisture content. For example, a fivefold increase in dry density from 160 to 800 kg/m³ results in thermal conductivity change from 0.0561 to 0.169 W/m K. At a dry density of 160 kg/m³, moisture change from 0 to 20% results in a change of thermal conductivity from 0.0561 to 0.0705 W/m K. A table listing values of thermal conductivity of different wood species is provided by Murty Kanury and Blackshear (1970). Additional references on the subject may be found in Pratt (1969).
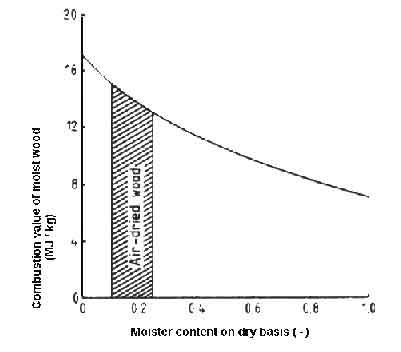
Figure:4 Changes in physical quantities during different stages of air drying.
The second property is that of permeability of wood - a consequence of the grainy structure of wood. This property also shows a strong dependence on the direction of flow considered. Permeability for flow parallel to the grain of wood could be 10$ times that for flow perpendicular to the grain (Roberts 1971).
These last two properties are crucial in understanding and developing a theory for the burning of wood.